Příklad 1 - Nerovnice
V kartézské soustavě souřadnic zobrazte graf relace pro níž platí:
(a) 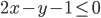
|
(b) 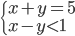
|
||
(c) 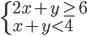
|
(d) 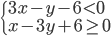
|
||
(e) 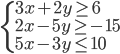
|
(f) 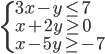
|
||
(g) 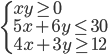
|
(h) 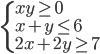
|
||
(i) 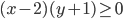
|
(j) 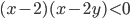
|
||
(k) 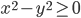
|
(l) 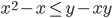
|
Příklad 2 - Rovnice s absolutní hodnotou
V kartézské soustavě souřadnic zobrazte graf relace pro níž platí:
(a) 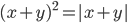
|
(b) 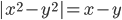
|
||
(c) 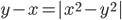
|
(d) 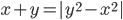
|
||
(e) 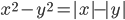
|
(f) 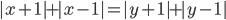
|
||
(g) 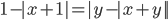
|
(h) 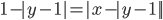
|
||
(i) 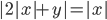
|
(j) 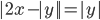
|
||
(k) 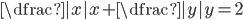
|
(l) 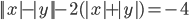
|
||
(m) 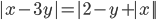
|
(n) 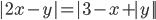
|
||
(o) 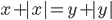
|
(q) 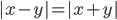
|
||
(r) 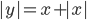
|
Příklad 3 - Nerovnice s absolutní hodnotou
V kartézské soustavě souřadnic zobrazte graf relace pro níž platí:
(a) 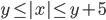
|
(b) 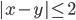
|
||
(c) 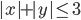
|
(d) 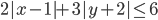
|
||
(e) 
|
(f) 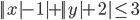
|
||
(g) 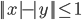
|
(h) 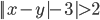
|
||
(i) 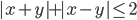
|
(j) 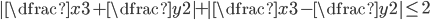
|
||
(k) 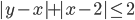
|
(l) 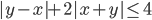
|
||
(m) 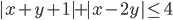
|
(n) 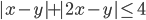
|
||
(o) 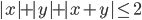
|
(p) 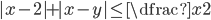
|
||
(q) 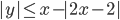
|
(r) 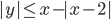
|
||
(s) 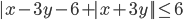
|
(t) 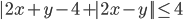
|
Příklad 4 - Soustavy s absolutní hodnotou
V kartézské soustavě souřadnic zobrazte graf relace pro níž platí:
(a) 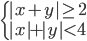
|
(b) 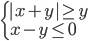
|
||