Příklad 1 - KRUŽNICE
V kartézské soustavě souřadnic zobrazte graf relace pro níž platí:
(a) 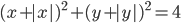
|
(b) 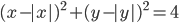
|
||
(c) 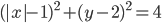
|
(d) 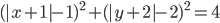
|
||
(e) 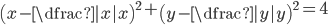
|
(f) 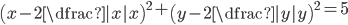
|
||
(g) 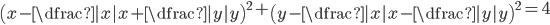
|
(h) 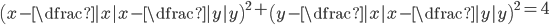
|
||
(i) 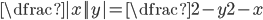
|
(j) 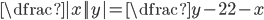
|
||
(k) 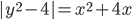
|
(l) 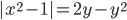
|
||
(m) 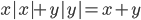
|
(n) 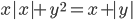
|
||
(o) 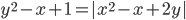
|
(p) 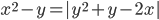
|
||
(q) 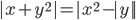
|
(r) 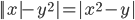
|
||
(s) 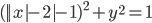
|
(t) 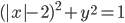
|
Příklad 2 - OSTATNÍ KUŽELOSEČKY
V kartézské soustavě souřadnic zobrazte graf relace pro níž platí:
(a) 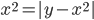
|
(b) 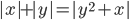
|
||
(c) 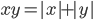
|
(d) 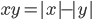
|
||
(e) 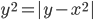
|
(f) 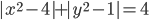
|
||
(g) ![\left[y-\sqrt{1-(|x|-1)^2}\right]\cdot\left[y+3\sqrt{1-\dfrac{|x|}{2}}\right]=0](http://grafy.rubesz.cz/wp-content/plugins/latex/cache/tex_3bc280c1e04614e8d04510ae3b20cdf4.gif)
|
(h) 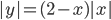
|
||
(i) 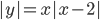
|
(j) 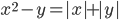
|
||
(k) 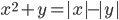
|
(l) 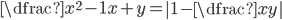
|
||
(m) 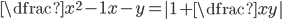
|
(n) 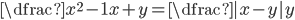
|
||
(o) 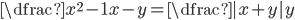
|
(p) 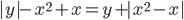
|
||
(q) 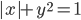
|
(r) 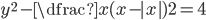
|
||
(s) 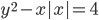
|
(t) 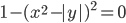
|
||
(u) 
|
Příklad 3 - Nerovnice
V kartézské soustavě souřadnic zobrazte graf relace pro níž platí:
(a) 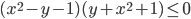
|
(b) 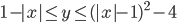
|
||
(c) 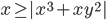
|
(d) 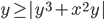
|
||
(e) 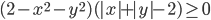
|
(f) 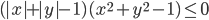
|
||
(g) 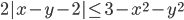
|
(h) 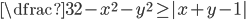
|
||
(i) 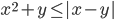
|
(j) 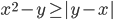
|
||
(k) 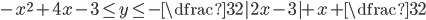
|
(l) 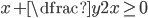
|
||
(m) 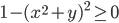
|
(n) 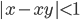
|
||
(o) 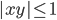
|
(q) 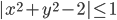
|
Příklad 4 - Soustavy
V kartézské soustavě souřadnic zobrazte graf relace pro níž platí:
(a) 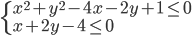
|
(b) 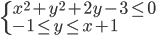
|
||
(c) 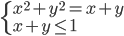
|
(d) 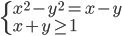
|
||
(e) 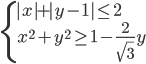
|
(f) 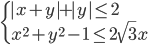
|
||
(g) 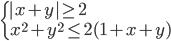
|
(h) 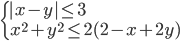
|
||
(i) 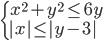
|
(j) 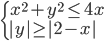
|
||
(k) 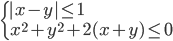
|
(l) 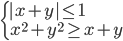
|
||
(m) 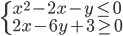
|
(n) 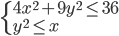
|
||
(o) 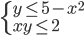
|
(p) 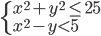
|
||
(q) 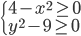
|
(r) 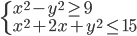
|